We lose the depth information due to planar projection.

So towards the stereo vision
Rays originating from the camera’s relative position C1 and C2 clearly intersect at a unique point, point X itself. This is called triangulation. We say we triangulated point X.




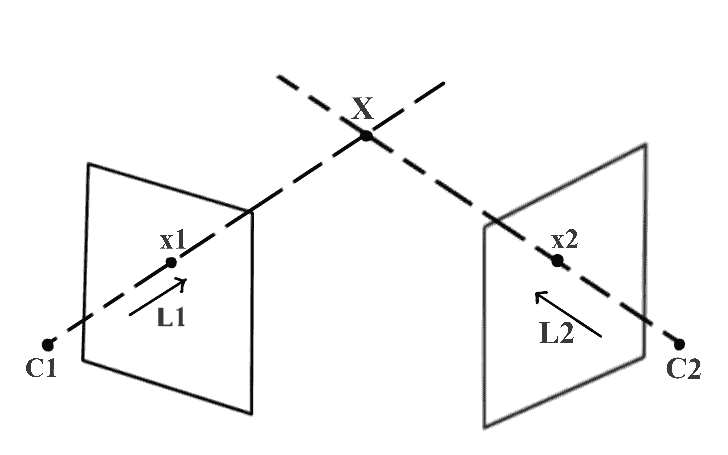
camera’s relative position         (be c1, c2) 
point correspondence             (be x1, x2) - projection of the same 3D point
direction vectors                 (be l1,l2) 

Consider one camera position as (0,0,0) - origin 
Stereo calibration to find the relative position of both cameras
Identify the corresponding points:
    1. Oriented FAST and rotated BRIEF (ORB) 
    disadvantage:  
        the ratio of the number of pixels with known point correspondence to the total number of pixels is minimal
    2. Pixels with similar neighboring pixel information
    disadvantage: 
        results in a single pixel from one image having multiple matches in the other image
    3. epipolar geometry
        an epipole is the image of the camera center of one view in the other view
        The line joining the two camera centers is called a baseline
        Fundamental matrix
    4. stereo disparity. It is similar to stereopsis or stereoscopic vision
    The more the shift closer is the object. This shift is what we call as disparity.
    Disparity = x – x’ = Bf/Z
    Where B is the baseline (Distance between the cameras), and f is the focal length.